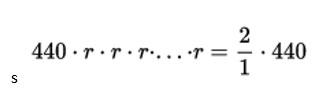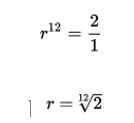"מוזיקה שמיימית" – THE MUSIC OF THE SPHERES
-----------------------------------------------------------------------
אנו מכבדים זכויות יוצרים ועושים מאמץ לאתר את בעלי הזכויות בצילומים המגיעים לידינו. אם זיהיתם בפרסומינו צילום שיש לכם זכויות בו, אתם רשאים לפנות אלינו ולבקש לחדול מהשימוש באמצעות כתובת המייל: rentatar@gmail.com - שלחו כאן אימייל
מאת – ספיר רודד
תוכן עניינים
מוזיקת הספירות
המוזיקה היא חלק בלתי נפרד מחיינו והיא השפה האוניברסלית של הטבע. הצליל הנשמע נתפס כביטוי של הסדר האלוהי – יחסים הרמוניים הבונים את היקום.
מהם אותם יחסים הרמוניים?
על פי החכמה העתיקה, מאחורי המוסיקה הנשמעת מסתתרים חוקים שעל פיהם בנוי העולם כולו. אלו הם חוקים שאם נלמד אותם ונעמיק בהם, נוכל אולי להגיע לתובנות חדשות על עצמנו, על הקשר שלנו לאנשים אחרים ועל הקשר שלנו לעולם. מהם אותם חוקים? אילו סודות יכולה המוזיקה ללמד אותנו? ומהי מוזיקת הספירות?
את המונח "מוזיקת הספירות" קבע פיתגורס- עוד במאה ה-16 לפנה"ס. פיתגורס היה הראשון שהגדיר באופן מדעי את הקשר שבין צליל, מספר ויחס מתמטי. על פי תפיסתו, ישנם חוקים אנלוגיים בין הטבע, האדם והמוזיקה. חוקים אלו אפשר לצמצם לפרופורציות מתמטיות או ליחסים מספריים. כיצד? הוא וחבריו השתמשו בכלי פשוט שנקרא- "מונוקורד" (מונו- יחיד קורד- אקורד)- פיסת עץ ועליה מתוח מיתר אחד- והוא גילה שבכל מיתר מסתתרים עוד הרבה צלילים חבויים ששונים מהצליל המקורי . פיתגורס קרא לזה "הרמוניות," ובעצם- אלה הם הצלילים העילאיים (או "הרמוניקות"), ה"Over Tones". פיתגורס השווה את היקום למונוקורד אחד ענק , עם מיתר שמחבר בין הרוח לחומר. הוא טען שהקשר ההרמוני קיים בכל חוקי הטבע ואכן- המדע המודרני אישר את טענתו (כוכבי הלכת, למשל, מפיקים צליל בתדירות מאד נמוכה). התורה הזו התפתחה לתורת "המיתרים", לתורת "העל-מיתרים" ובשנת 1995- לתורת M שאומרות שהחלקיקים הקטנים ביותר ביקום עשויים ממיתרים רוטטים רב–מימדיים כלומר: היקום הוא כלי נגינה אחד גדול! נכון להיום עוד לא נימצא ניסוי שאישר את התאוריה הזו אבל יודעים דבר אחד – היקום מורכב מגלים של חומר שניתן למדוד את האנרגיה המופקת מהם כי הכל סביבנו ובתוכנו נמצא בתנועה מתמדת וכל תנודה – Vibration,Vibes – מניבה צליל .
בין צלילים ומספרים
במאה ה-6 לפני הספירה גילה פיתגורס כי יש קשר בין צירופי צלילים הרמוניים ובין מספרים. הוא הראה כי למתמטיקה יש תפקיד גדול באופן שבו המוזיקה נשמעת: כאשר יחסי תדירויות התווים הם כיחס פשוט בין שני מספרים שלמים אז מתקבלים צירופי צלילים הרמוניים.
בסולם הפיתגוריאני היחס בין התווים הוא 3 ל-2. כלומר: ניתן להתחיל מכל תו ולחשב את התווים האחרים ע"י הכפלת התדירות של התו ב-3/2.
כאשר כלי נגינה מפיק צליל מסוים, הוא גורם לרטט האוויר המקיף אותו. תנודות אלו מועברות בצורת גלי לחץ דרך האוויר, עד אשר הן מגיעות לאוזנינו ונקלטות במוח כצליל.
פיתגורס האמין כי מאחר שגוף בתנועה יוצר תנודות באוויר ומפיק צלילים אז גם תנועתם של כוכבי הלכת סביב השמש אמורה להפיק צליל ויותר מזאת, בגלל היחסים בין התדירות של מסלול התנועה שלהם, הוא טען כי הצלילים האלו ייצרו הרמוניה.
קפלר היה מרותק מהרעיון כי גופים שמימיים "מנגנים הרמוניה" מה שהוביל אותו להנחה כי הגופים "שרים" כאשר מקיפים את השמש. הוא העביר שנים במחקר על מנת לגלות יחסים הרמוניים בין זמני המחזור של מסלול ההקפה של כוכבי לכת סביב השמש. הוא כתב ספר שלם אודות המחקר שלו שנקרא " harmonices mundi " (הרמוניה אוניברסלית) שם הוא מתאר בין היתר כיצד גילה את זמני המחזור האמתיים של הכוכבים ומכאן הניח כי מסלול ההקפה שלהם הוא בעצם אליפטי.
מאחר שגלי קול מכניים עוברים דרך חומר, לא ניתן לאמת את התאוריה שגופים שמימיים מייצרים מנגינה הרמונית, מאחר והחלל הוא ריק.
למה התכוון פיתגורס כשטען שקיימת הרמוניה במערכת השמש?
האם התכוון שמאחר שלכל גוף שמימי יש מסלול תנועה ייחודי ומאחר שכל תנועה מפיקה קול, אז לכל גוף שמימי יהיה את הצליל הייחודי שהוא מפיק? והקשר בין כל הצלילים האלו ייצור הרמוניה ?
או שהוא התכוון כי קיימים יחסים מתמטיים בין תנועת הכוכבים אשר יוצרים דפוס הרמוני?
במוזיקה, אנו יודעים ש"מרווח" מוגדר כיחס בין התדירויות. ניתן להתייחס להרמוניה המוזיקלית עליה פיתגורס וקפלר דיברו כהקבלה המתארת את היחסים של התדירויות בתנועת הכוכבים סביב השמש ולבחון האם באמת יחסים אלו מייצגים יחסים של הרמוניה מוזיקלית .
שיטת הכוונון המושווה היא שיטה לכוונון כלים מוזיקליים לפי חלוקת מרווחים הבנויה מחצי טונים זהים.
האוקטבה מוגדרת כיחס של 1:2, כלומר, צליל במרווח של אוקטבה מהתו לה (440 HZ) יהיה בתדירות של 880 HZ.
חלוקת האוקטבה למרווחים שווים:
מספר התווים במוזיקה המערבית הוא 12.
בכדי לחלק את האוקטבה למרווחים שווים עלינו למצוא את הערך שכאשר נכפיל אותו בתדירות התו (לדוגמא : לה- 440 הרץ ) 12 פעמים נקבל ערך ששווה ביחס של 2:1 (880 HZ) וייתן לנו את התו לה באוקטבה הבאה (מרווח של 12 תווים)
מאחר ומרווח מוגדר כיחס בין התדירויות ולא כהפרש ביניהם נקבל קשר של סדרה הנדסית.
נחפש את המרווח שכאשר נפעיל אותו על התו לה 12 פעמים נקבל את התו לה במרחק אוקטבה. במילים אחרות, אנו מחפשים את המרווח שכאשר יוכפל בעצמו 12 פעמים ייתן בדיוק את המרווח אוקטבה (יחס של 2:1)
היחס שקיבלנו הוא יחס זה נקרא חצי טון ו- 12 חצאי טון הם אוקטבה אחת.
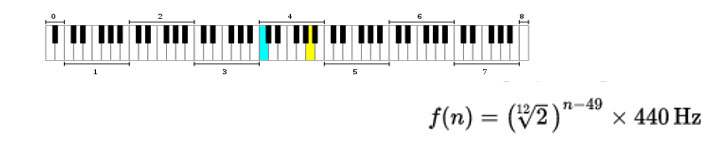
תדירויות תווים בפסנתר
זוהי משוואה המייצגת את הקשר בכוונון מושווה בין התדירויות לתווים בפסנתר מודרני אידאלי של 88 קלידים. במרווחים שווים של שתיים עשרה טונים. כאשר הקליד מספר ה 49 הוא התו לה (באוקטבה הרביעית) אשר מכוון ל 440 הרץ.
במאה החמישית לפני הספירה המתמטיקאי פיתגורס גילה שהמרווחים שנשמעים נעים במיוחד לאוזן הם 2:1 ו – 3:2. מרווח של 2:1 אנו כבר מכירים כמרווח אוקטבה, מרווח של 3:2 נקרא קווינטה. ניתן לראות שבשיטת הפסנתר המושווה המרווח 2:1 מופיע כ-12 חצאי טון, אך האם אנו יכולים להגיע ליחס של 3:2? מסתבר שלא ניתן להגיע ליחס זה באמצעות חלוקת האוקטבה למרווחים שווים, אך אם נחלק את האוקטבה ל-12 מרווחים, נקבל שמרווח של 3.5 טון (7 חצאי טון) יוצא קרוב מאוד ל 3:2.
מרווח זה מספיק קרוב לשלושה חצאים כדי שהאוזן האנושית לא תוכל להרגיש בהבדל, לכן מחלקים את האוקטבה ל-12 מרווחים שווים.
תדירויות כוכבי הלכת והתווים המייצגים אותם בשיטת הכוונון המשווה
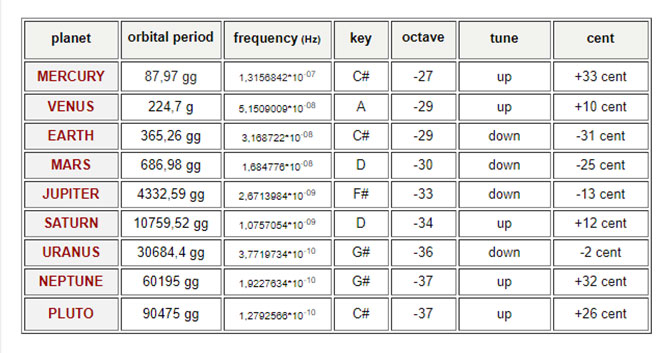
מאחר שתדירויות זמני המחזור של תנועת הכוכבים נמוכות מידי בכדי להיות מיוצגות באוקטבות של פסנתר מודרני, עלינו להעלות אותם בכמה אוקטבות על מנת שיתאימו למבנה הפסנתר. ( אך היחסים בין המרווחים נשמרים )
*עמודת הCENT מייצגת את מספר מאיות חצי הטון ( כ"כ זניח שלא ניתן להבחין בשינוי באוזן האנושית ) שעלינו להעלות או להחסיר מהתוצאה שקיבלנו על מנת להגיע לתו קיים ( לא קיים תו בפסנתר שמורכב ממאית חצי הטון ) זאת בעקבות שיטת הכוונון המושווה שמחלקת את התווים לחצאי טונים
סרטון NASA – צלילים בחלל החיצון
היום ידוע כי כוכבי לכת מפיקים צליל, אמנם בחלל לא ניתן לשמוע צלילים מאחר והריק (העדר חומר) לא מאפשר מעבר של גלי קול אך הפרשי המתחים באטמוספרות של כוכבי הלכת יוצרים גלים אלקטרומגנטיים שניתן להמיר אותם לגלי קול בטווח השמיעה האנושית. וזה מה שנאס"א עשו בהקלטות המוצגות :
על מנת לחשב את גלי ה elf המופקים מהאטמוספרה האלקטרומגנטית של כוכבי לכת עלינו לזהות פעילות חשמלית (ברקים) שנובעים מפריקת המתח החשמלי בשדה האלקטרומגנטי
קיומם של ברקים בכוכבי לכת במערכת השמש נצפו במשימות של נאס"א ועלינו לחשב את התדר של גלי הelf שכל כוכב לכת מפיק על מנת למצוא את התהודה האלקטרומגנטית שלו .
בהמשך ניתן לבדוק את התדר האלקטרומגנטי של כל כוכב ולבדוק גם שם האם מתקיימת הרמוניה. ולאחר מכן להשוות בין התדר האלקטרומגנטי לבין התדר הזוויתי בכדי לאמת או לשלול קשר בין אלו.
“There is geometry in the humming of the strings, there is music in the spacing of the spheres.”
Pythagoras
פעילות
כמה מרווחים הרמוניים ניתן להרכיב מהתווים:
-דו דיאז
-לה
-פה דיאז
-סול דיאז
-רה
*בטבלה מופיעים מרווחים של 3 אוקטבות שונות (רה, סול דיאז, דו דיאז)
Calter, Paul. "Pythagoras & Music of the Spheres". Geometry in Art & Architecture. Dartmouth College. Retrieved November 26, 2011.
לאחר מבצע החיסול של חסאן נסראללה בדאחייה בבירות עם פצצות חודרות בונקרים מצאנו לנכון להבהיר מהן פצצות אלו ההסטוריה של - קראו עוד
בעקבות הודעת החותים השבוע על ירי של טיל היפרסוני לכיוון ישראל בחרנו להרחיב מעט על הטיל, הטכנולוגיה הצבאית עברה שינויים - קראו עוד
כרטיסי ביקור דיגיטליים הפכו לטרנד בקרב עובדי ההיטק בעולם ועכשיו כבר כל עסק רוצה כרטיס ביקור דיגיטלי.
כתם שמש הוא אזור על פני השמש אשר מתרחשות בו מערבולות מגנטיות רבות עוצמה. הטמפרטורה באזור זה נמוכה יחסית לסביבתו - קראו עוד
בטבע קיימים 3 מצבי צבירה : מוצק, נוזל, גז . ניתן להעביר חומרים ממצב צבירה אחד למצב אחר, באמצעות קירור - קראו עוד
מהיא תקשורת המונים והמרכיבים של תקשורת המונים, פרסום של עניין ציבורי ייעשה אך ורק כאשר יש לציבור עניין מהי עבירה - קראו עוד
כשמזכירים את המונח כור גרעיני, הדבר הראשון שעולה לראש הוא בדרך כלל נשק גרעיני, אבל רובם הגדול של הכורים בעולם - קראו עוד
תהליך הפענוח של מבנה האטום ארך שנים רבות מאוד ורק ועם התפתחות הטכנולוגיה אפשר היה לחקור את האטום לעומק
חלקיקי המוצק נמשכים זה לזה ותנועת החלקיקים של המוצק המודגמת כאן מתארת חלקיקים הרוטטים סביב מקומם.
כתוצאה מסיבוב האלקטרון סביב הגרעין, פועל על האלקטרון כח צנטרפוגלי המושך את האלקטרון החוצה בדומה לכח הפועל ילד המסתובב על - קראו עוד
המולקולות של כל החומרים נעות בהתמדה. הן נעות בכל הכיוונים באקראי, מתנגשות אלו באלו, ותוך כדי כך הן מתפזרות באחידות - קראו עוד
האטום, ביוונית עתיקה פירושו בלתי ניתן לחלוקה, הוא אבן הבניין של כל החומר. בתקפה העתיקה היו ויכוחים רבים בנוגע למהות - קראו עוד
